The fastest way to convert the binary into decimal using a table

Sometimes we need to match the binary number to the decimal number. But for people like me who is not that sensitive to binary, it seems they are all the same… So I need to write a table to match them. It is easy since binary has only 2 digits, 0 or 1. But the calculation could be nasty, and the layout would be annoying when the quantity gets bigger. And when the layout gets annoying, we will make mistakes. And nobody loves mistake.

But there is a simple way we can make this procedure in to a no-brainer. Let’s write down a 4-bits binary and decimal match table. Just check the one below. It is simple, isn’t it? Do you find any pattern?

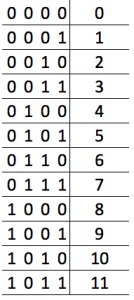
If you don’t, just don’t review it by row, instead, review it by column, and pay attention to the 0. Let me color it for you. So you can figure it out.

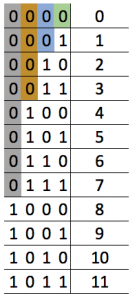
The pattern is:

the number of zero in a column will always equal to the power of 2!

This means, for the binary part of this table:

• In the 1st column, the number will always be 0 1 0 1 0 1 0 1 0 1 0 1…
• In the 2nd column, the number will always be  00 11 00 11 00 11 00 11…
• In the 3rd column, the number will always be 0000 1111 0000 1111…
• In the 4th column, the number will always be 00000000 11111111 00000000 11111111…
• ……
• for each column, after matching each pattern for 0, there will always be equal number of 1. So, take the 4th row for instance, if there are eight ‘0’, there must be eight ‘1’ come after.

So, every time you need to write down a match table, instead of writing number in a row, and do a binary calculation for the next row. You just need to write 0 down in column,then you fill the rest with 1. It will be very easy. So, for a single pattern:

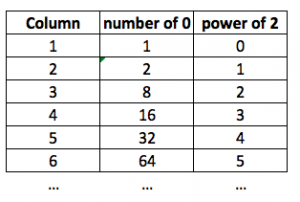Now, every one is happy :) We don’t need our brain in this scenario anymore and that is good, people are lazy -_-

 

Thanks for reading!

Follow me (albertgao) on twitter, if you want to hear more about my interesting ideas.