10 questions you must know for doing linear regression using gradient descent
When you start to learn machine learning, linear regression is most likely to be the your best candidate. Not only because you can re-use the according concepts in statistics, but also you can understand many foundation concept which can be adopted to other machine learning algorithms. I think the most efficient way to learn something is by asking questions, and this is why I wrote this blog. After this blog, even you still have some questions, but I think you will have that knowledge-tree to further dig into.
What problem does linear regression tend to solve?
To find a best fitting line for a scatter plot. Let’s say you have a set of data, where the x-axis represents the year of a house and the y-axis represents the selling price of the house. After finding the best fitting line, you can easily answer the question like What is the price for house which built in a random year.
So, what do we start with?
We need to have some training examples. They are the data you use to find that line.
How do we use it?
Pass into a learning algorithm
What happen next?
- Algorithm outputs a function
h(x). whereh = hypothesis - This function takes an input, output the estimated value
How do we represent it?
hꝊ(x) = Ꝋ0 + Ꝋ1 * x- Tip: univariate linear regression = linear regression with one variable
So in summary
- A hypothesis takes in some variable
- Uses parameters determined by a learning system
- Outputs a prediction based on that input
OK. Now we have an equation with variables we don’t know, how to solve it?
The answer is, using a cost function.
What is a cost function?
- A cost function lets us figure out how to fit the best straight line to our data.
- Based on our training set we want to generate parameters which make the straight line chosen these parameters so
hθ(x)is close toyfor our training examples - That is to say, it is a way to, using your training data, determine values for your
Ꝋvalues which make the hypothesis as accurate as possible - In other words, it is a function of the parameters of
Ꝋ, hypothesis is a function ofx
To formalize this;
- We want to want to solve a minimization problem
- Minimize
(hθ(x) - y)^2- i.e. minimize the difference between
h(x)andyfor each/any/every example - minimizes the sum of the squared errors of prediction.
- Sum this over the training set:
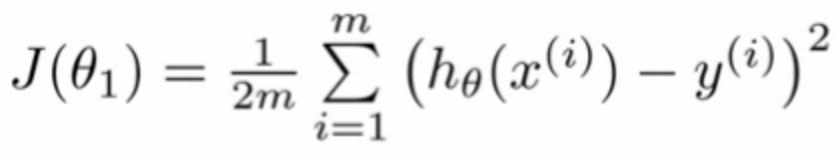
- i.e. minimize the difference between
How to find the best θ?
- using
Gradient descent - the gradient of a function is a
vectorwhich points towards the direction of maximum increase. Consequently, in order to minimize a function, we just need to take the gradient, look where it’s pointing, and head the other direction.
How to do the gradient descent?
Gradient descent can be succinctly described in just a few steps:
Choose a random starting point.
Each time you change the parameters
θa little bit to try reducing the cost functionJ(θ1,θ2)- Take the gradient of your cost function at your location.
- moving towards the minimum (down) will great a negative derivative, the learning rate alpha will always positive, so will update cost function
Jto a smaller value. - When you get to the minimum point, the gradient of tangent(derivative) is 0.
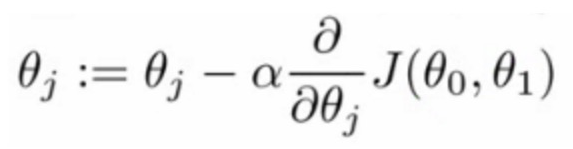
Repeat until we converge to a local minimum.
And the result would be?
Using gradient descent with a few hundred iterations, we can easily find parameters θ for our linear regression which give us a nice fit. (Note that there are faster algorithms than gradient descent, but they operate on the same basic principles!)
Follow me (albertgao) on twitter, if you want to hear more about my interesting ideas.
Thanks for reading!